Madhusudan Navandar
Lecturer in Computer Science and Mathematics, Ph No : 8123724274, 7975475011 E-Mail : madhunavandar@gmail.com
Wednesday, July 19, 2023
Sample Identity Card in HTML&CSS
Sunday, December 19, 2021
Accountancy Assignment for BCA I Semester in AME Science Degree College, Raichur.
Question 1:
Question 2:
Question 3:
Journalise the following transactions in the books of M/s. R.K. & Co.
(i) Purchased goods at list price of ₹ 20,000 from Vishal at 20% trade discount against cheque payment.
(ii) Purchased goods at list price of ₹ 20,000 from Naman at 15% trade discount against cash.
(iii) Purchased goods at list price of ₹ 30,000 from Amrit at 20% trade discount.
(iv) Purchased goods at list price of ₹ 40,000 for ₹ 35,000 for cash.
(v) Goods returned of list price ₹ 10,000 purchased from Amrit.
(vi) Sold goods to Parul at list price of ₹ 40,000 at 10% trade discount against cheque payment.
(vii) Sold goods to Aman at list price of ₹ 30,000 at 10% trade discount against cash.
(viii) Sold goods to Pawan at list price of ₹ 20,000 at 10% trade discount.
(ix) Sold goods to Yamini at list price of ₹ 25,000 for ₹ 23,000.
(x) Sold goods costing ₹ 10,000 at cost plus 20% less 10% trade discount to Bhupesh.
(xi) Sold goods purchased at list price of ₹ 50,000 less 15% trade discount sold at a profit of 25% & 10% trade discount against cheque.
(xii) Aman returned goods of list price of ₹ 10,000 sold to him at 10% trade discount.
Question 4.
Journalise the following transactions in the books of Bhushan Agencies:
(i) Received from Bharat cash ₹ 20,000, allowed him discount of ₹ 500.
(ii) Received from Vikas ₹ 35,000 by cheque, allowed him discount of ₹ 750.
(iii) Received from Akhil ₹ 38,000 in settlement of his dues of ₹ 40,000 in cash.
(iv) Received from Amrit ₹ 50,000 by cheque on account against dues of ₹ 60,000.
(v) Paid cash ₹ 40,000 to suresh, availed discount of 2%.
(vi) Paid by cheque ₹ 25,000 to Mehar and settled her dues of ₹ 26,000.
(vii) Paid ₹ 25,000 to Yogesh by cheque on account.
(viii) Purchased goods costing ₹ 1,00,000 against cheque and availed discount of 3%.
(ix) Purchased goods costing ₹ 60,000 from Akash & Co., paid 50% immediately availing 3% discount.
(x) Sold goods of ₹ 30,000 against cheque allowing 2% discount.
(xi) Sold goods of ₹ 60,000 to Vimal received 50% of due amount allowing 2% discount.
Question 5.
Journalise the following entries:
(i) Goods worth ₹ 500 given as charity.
(ii) Sold goods to Mayank of ₹ 1,00,000, payable 25% by cheque at the time of sale and balance after 30 days of sale.
(iii) Received ₹ 975 from Harikrishna in full settlement of his account for 1,000.
(iv) Received a first and final dividend of 60 paise in a rupee from the Official Receiver of Rajan, who owed us ₹ 1,000.
(v) Charged depreciation on plant ₹ 1,000.
(vi) Charge interest on Drawings ₹ 1,500.
(vii) Sold goods costing ₹ 40,000 to Anil for cash at a profit of 25% on cost less 20% trade discount and charged 8% Value Added Tax and paid cartage ₹ 100, which is not to be charged from customer.
Question 6:
Question 7:
Journalise the following transactions of Ram Delhi:
Question 8:
Circles Homework Sums Ex:10.2 - 4,5,9,10,11,13
Question 4.
Prove that the tangents drawn at the ends of a diameter of a circle are parallel.Solution:
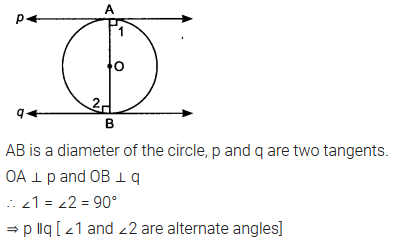
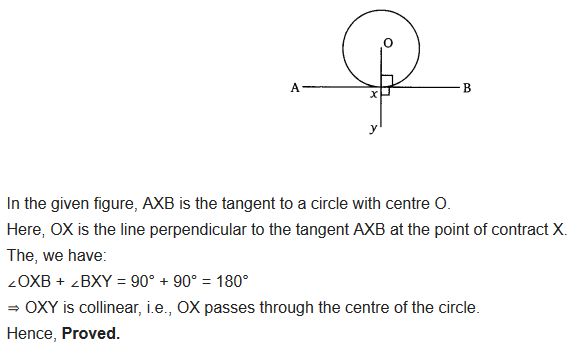
Prove that the perpendicular at the point of contact to the tangent to a circle passes through the centre.
Solution:
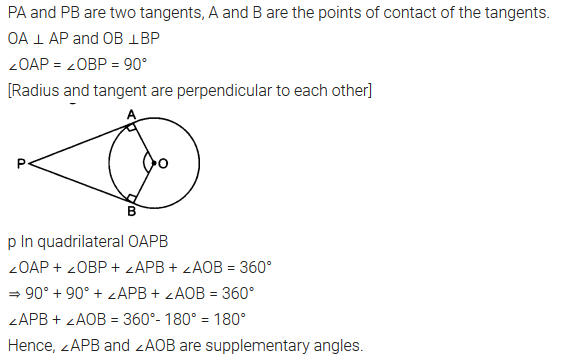
Prove that the angle between the two tangents drawn from an external point to a circle is supplementary to the angle subtended by the line segment joining the points of contact at the centre.
Solution:
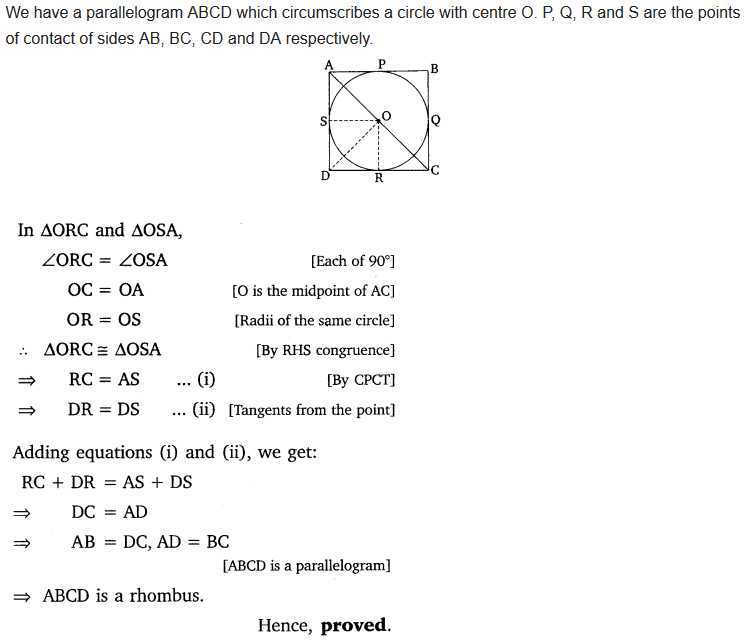
Prove that the parallelogram circumscribing a circle is a rhombus.
Solution:
In figure, XY and X’Y’ are two parallel tangents to a circle , x with centre O and another tangent AB with point of contact C intersecting XY at A and X’Y’ at B. Prove that ∠AOB = 90°.
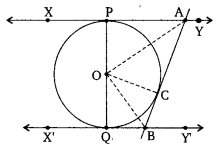
Solution:

Prove that the parallelogram circumscribing a circle is a rhombus.
Solution:

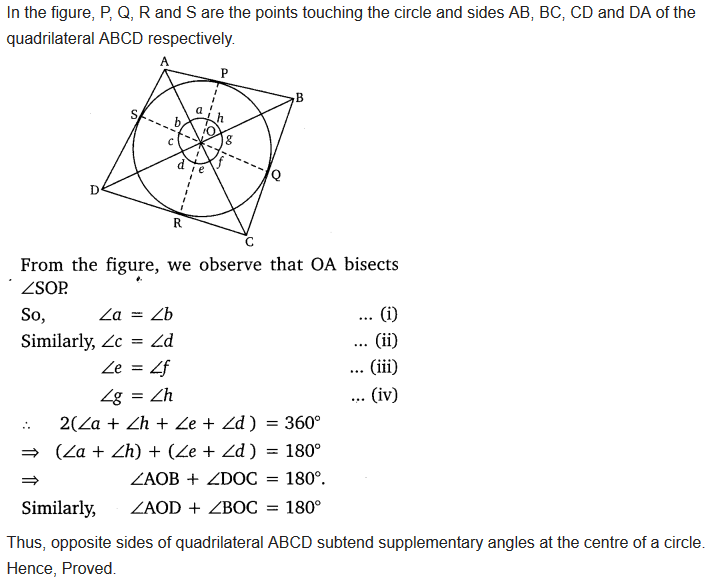
Prove that opposite sides of a quadrilateral circumscribing a circle subtend supplementary angles at the centre of the circle.
Solution:
Wednesday, December 15, 2021
Class 10 : Theorems on Circles
Theorem 1- The tangent at any point of a circle
is perpendicular to the radius through the point of contact.
Given: A
circle with centre O, a tangent XY at the point of contanct P.
To
prove: OP ⊥ XY.
Construction: Take a point Q, other than P or XY. Jion OQ.
Proof: Q
lies on the tangent XY.
Q lies outside the circle.
Let OQ cuts the circle at R.
OR < OQ (a part is less than a whole)
But, OR=OP (radii of the same circle)
So, OP < OQ
Thus, OP is shorter than any line segment
joining O to any point on XY other than point P.
Therefore, OP is the shortest distance
between O and line segment XY.
But, the shortest distance between a point
and a line segment is the perpendicular distance.
Therefore, OP is perpendicular to XY.
Sample Identity Card in HTML&CSS
<html> <head> <title>ID Card</title> <style> body { background: url(back.jpg) cent...

-
<html> <head> <title>ID Card</title> <style> body { background: url(back.jpg) cent...
-
B.COM I Semester, RUR. Office Aut😀mation Unit 1 Notes link







