Question 4.
Prove that the tangents drawn at the ends of a diameter of a circle are parallel.Solution:
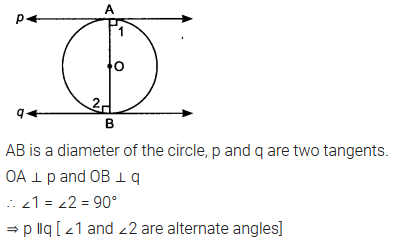
Question 5.
Prove that the perpendicular at the point of contact to the tangent to a circle passes through the centre.
Solution:
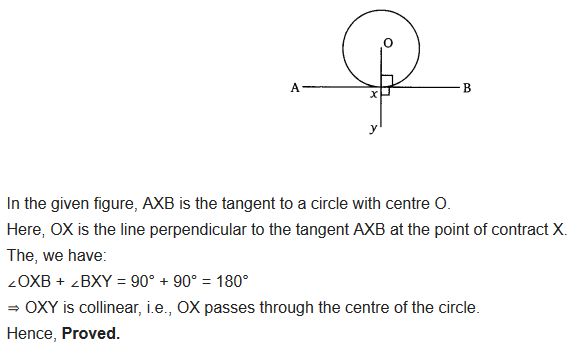
Prove that the perpendicular at the point of contact to the tangent to a circle passes through the centre.
Solution:

Question 10.
Prove that the angle between the two tangents drawn from an external point to a circle is supplementary to the angle subtended by the line segment joining the points of contact at the centre.
Solution:
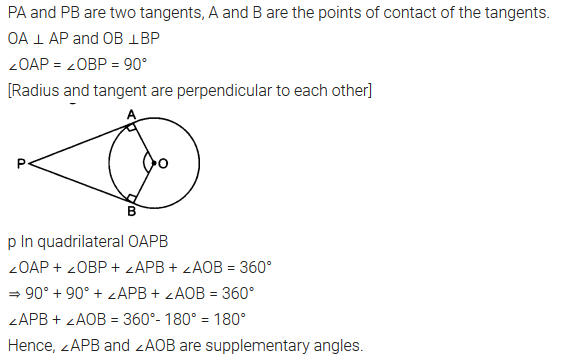
Prove that the angle between the two tangents drawn from an external point to a circle is supplementary to the angle subtended by the line segment joining the points of contact at the centre.
Solution:

Question 11.
Prove that the parallelogram circumscribing a circle is a rhombus.
Solution:
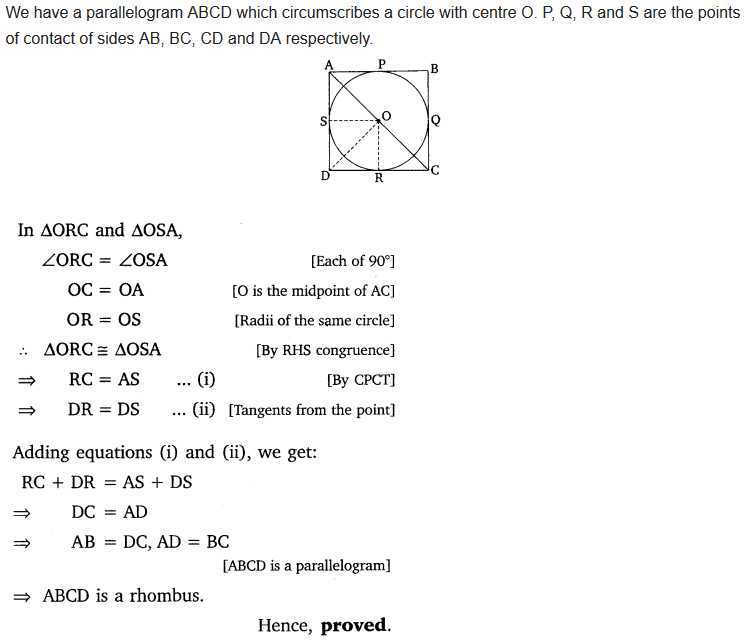
Prove that the parallelogram circumscribing a circle is a rhombus.
Solution:

Question 9.
In figure, XY and X’Y’ are two parallel tangents to a circle , x with centre O and another tangent AB with point of contact C intersecting XY at A and X’Y’ at B. Prove that ∠AOB = 90°.
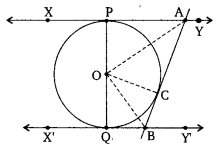
Solution:

In figure, XY and X’Y’ are two parallel tangents to a circle , x with centre O and another tangent AB with point of contact C intersecting XY at A and X’Y’ at B. Prove that ∠AOB = 90°.

Solution:

Question 11.
Prove that the parallelogram circumscribing a circle is a rhombus.
Solution:

Prove that the parallelogram circumscribing a circle is a rhombus.
Solution:

Question 13.
Prove that opposite sides of a quadrilateral circumscribing a circle subtend supplementary angles at the centre of the circle.
Solution:
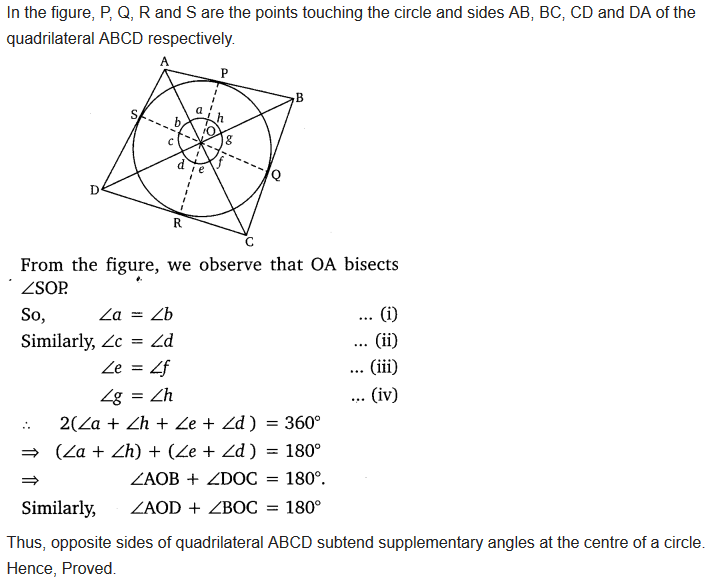
Prove that opposite sides of a quadrilateral circumscribing a circle subtend supplementary angles at the centre of the circle.
Solution:



No comments:
Post a Comment